Mathematics of zk-Snarks
I thought people would be interested in what’s going on under the hood in a relatively accessible way. What’s the process by which someone can prove they they possess some information without divulging that information?
There are many implementations of zk-SNARKs, or Zero-Knowledge Succinct Non-Interactive Argument of Knowledge. I’ll be covering the QAP variant here. Also, I’ve abstracted away some important nuances for the sake of making the concept and computation more accessible.
Lets say we want to prove that we know the solution for the equation below:
\[x^2 + 4 = 13\]First, we must flatten equation (1) into an arithmetic circuit with a sequence of steps that can take two forms. The first is:
\[b = a\]The second is:
\[b \ (op) \ c = a\]where $op$ $\in (+, -, \times, \div)$. The circuit for Equation (1) is:
\[\begin{equation} \begin{split} output_1 & = x \times x \\ output_2 & = output_1 + 4 \\ \end{split} \end{equation}\]Each step, $output_1$ and $output_2$, is called a constraint. In this case, there are two constraints. You’ll also hear them referred to as gates. We can visualize the process below.
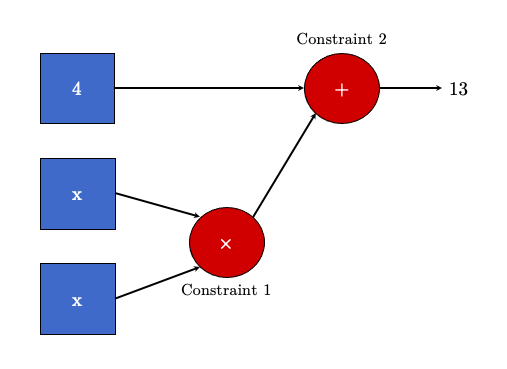
We convert our arithmetic circuit into a rank-1 constraint system (R1CS). The R1CS is a triplet of vectors, $(\vec{l_i}, \vec{r_i}, \vec{o_i})$, which when used with a solution vector $\vec{s}$, will allow us to solve each constraint, $i$.
\[\langle \vec{l_i}, \vec{s} \rangle \times \langle \vec{r_i}, \vec{s} \rangle = \langle \vec{o_i}, \vec{s} \rangle\]To create these vectors, we must first create a map which dictates the location of all variables used to solve our equation. Below is the one we will use:
\[\vec{s} = \begin{bmatrix} 1 & x & output_1 & output_2 \end{bmatrix}\]We include 1 as a dummy variable. Since we know $x$ is equal to 3, the solution vector will look like this. A valid solution vector is proof of proper circuit execution.
\[\vec{s} = \begin{bmatrix} 1 & 3 & 9 & 13 \end{bmatrix}\]To solve the first constraint (3 x 3 = 9), we use our map to create three vectors corresponding to $\vec{l_1}$, $\vec{r_1}$, and $\vec{o_1}$.
\[Constraint_1 \begin{cases} \vec{l_1} = \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}\\ \vec{r_1} = \begin{bmatrix} 0 & 1 & 0 & 0 \end{bmatrix}\\ \vec{o_1} = \begin{bmatrix} 0 & 0 & 1 & 0 \end{bmatrix}\\ \end{cases}\]We multiply our $\vec{l_1}$, $\vec{r_1}$ and $\vec{o_1}$ vectors by the solution vector elementwise and take the sum. The sum of $\vec{l_1}$ times the sum of $\vec{r_1}$ should equal the sum of $\vec{o_1}$.
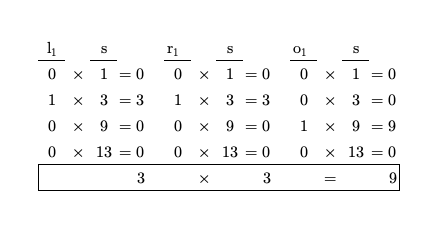
Below are the final vectors for the second constraint:
\[Constraint_2 \begin{cases} \vec{l_2} = \begin{bmatrix} 4 & 0 & 1 & 0 \end{bmatrix} \\ \vec{r_2} = \begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix} \\ \vec{o_2} = \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix} \\ \end{cases}\]Next, we convert our R1CS to QAP (Quadratic Arithmetic Program) form. In other words, we want to represent it as a system of polynomials. We first look at $\vec{l_1}$ and $\vec{l_2}$. For $\vec{l_1}$, the first value is 0 so the point is (1, 0). For $\vec{l_2}$, the first value is 4 so the point is (2, 4). To create the polynomial you typically use Lagrange Interpolation but our example is simple enough that elementary algebra suffices.
\[\underbrace{(1, 0)}_{\text{(constraint num, first value in $l_1$)}}\] \[\underbrace{(2, 4)}_{\text{(constraint num, first value in $l_2$)}}\] \[slope = \frac{Rise}{Run} = \frac{4-0}{2-1} = \frac{4}{1} = 4\] \[\begin{aligned} 4(1) + y &= 0 \\ y &=-4 \end{aligned}\]The resultant equation is:
\[4x-4\]If we do this for for all $l$, $r$, and $o$, we come up with a system of polynomials which are shown below. For L, R and O the number of equations in each set should equal the number of values in our solution vector. In our case, there are four.
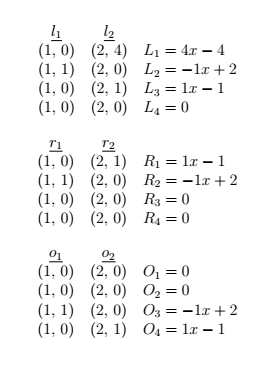
Now that we have a system of polynomials, we want to condense this even further to a set of three polynomials: $L(x)$, $R(x)$ and $O(x)$. To do this, we multiply the solution vector by our polynomials and take the sum for $L$, $R$ and $O$.
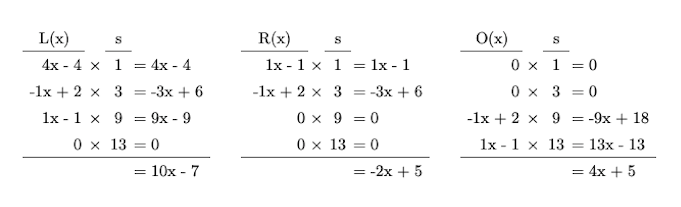
Therefore:
\[\begin{aligned} L(x)&=10x-7 \\ R(x)&=-2x+5 \\ O(x)&= 4x+5 \end{aligned}\]We know that:
\[O(x) = L(x) \times R(x)\]Therefore:
\[P(x) = L(x) \times R(x) - O(x) = 0\]Since $P(x)$ is a polynomial, it is divisible by:
\[Z(x)=(x-1)(x-2) \ldots\ (x-n_c)\]where $n_c$ is the number of constraints. In our case, $n_c = 2$ which becomes:
\[\begin{align} Z(x) & = (x-1)(x-2)\\ \end{align}\]If we divide $P(x)$ by $Z(x)$ we get an $H(x)$:
\[\frac{P(x)}{Z(x)} = \frac{L(x) \times R(x) - O(x)}{Z(x)} = H(x)\]such that $H(x)$ has no remainder. So, we first need to solve for P(x):
\[P(x) = (10x-7) \times (-2x+5) - (4x+5) = -20x^2+60x-40\]Then we solve for $H(x)$ by dividing $P(x)$ by $Z(x)$. We see there is no remainder so we’ve proven that we have the correct solution vector and we’ve completed the arithmetic circuit.
\[H(x) = \frac{P(x)}{Z(x)} = \frac{-20x^2+60x-40}{x^2-3x+2} = -20\]So how can we send this over to the verifier without leaking any of this information? Abstracting away from the cryptography and some other things, we simply encrypt $L(x)$, $R(x)$, $O(x)$ and $H(x)$ and send it to the verifier who also has an encrypted $Z(x)$.